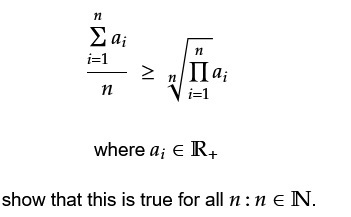
![]()
You are first introduced to proof by induction in the first year of A-level further mathematics.
A statement such as: “![]() is a prime number, where
is a prime number, where ![]() is a natural number” may be true for some values of
is a natural number” may be true for some values of ![]() and false for others.
and false for others.
You can prove a statement ![]() is true for all natural numbers
is true for all natural numbers ![]() , by showing
, by showing ![]() satisfies two conditions:
satisfies two conditions:
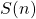 is true when
is true when 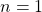
- Under the assumption
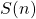 is true when
is true when 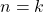 , it follows that
, it follows that 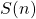 } is true when
} is true when 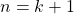 .
.
From these two conditions it follows that ![]() is true for all
is true for all ![]() .
.
Most problems encountered at A-level can be dealt with relatively easily. However, proof by induction problems do exist where the above two conditions are quite difficult to prove and require a lot of work, unless you’ve encountered the problem before.
You’ll now learn a variant of proof by induction which can simplify the work considerably.
We will prove a statement ![]() is true for all natural numbers
is true for all natural numbers ![]() , by showing
, by showing ![]() satisfies three conditions:
satisfies three conditions:
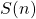 is true when
is true when 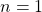
- Under the assumption
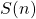 is true when
is true when 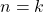 , it follows that
, it follows that 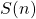 } is true when
} is true when 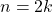 .
. - Under the assumption
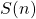 is true when
is true when 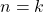 , it follows that
, it follows that 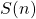 } is true when
} is true when 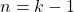 .
.
This is sometimes called forwards-backwards induction. Think carefully why these three conditions prove ![]() for all natural numbers. The second condition proves it for larger and larger ‘doubled values’, and the third condition ‘fills in’ all the gaps we left behind, thus hitting all the numbers.
for all natural numbers. The second condition proves it for larger and larger ‘doubled values’, and the third condition ‘fills in’ all the gaps we left behind, thus hitting all the numbers.
Consider the well know arithmetic-geometric mean inequality:
(1) ![Rendered by QuickLaTeX.com \begin{equation*} {\displaystyle \frac{{\textstyle \sum\limits _{{\textstyle i=1}}^{n} a}{\displaystyle _{i}}}{n} \ \geq }{\textstyle \ \sqrt[n]{\prod\limits _{i=1}^{n}} a_{i}} \end{equation*}](https://www.maxbenjamintutor.com/wp-content/ql-cache/quicklatex.com-c53c1e2c04b48e46c59a661c9df47854_l3.png)
where ![]()
We want to show that this is true for all ![]() .
.
For ![]() , we have
, we have ![]() . So the first condition is met.
. So the first condition is met.
Next, assume true for ![]() ,
,
![Rendered by QuickLaTeX.com \begin{equation*} {\displaystyle \frac{{\textstyle \sum\limits _{{\textstyle i=1}}^{k} a}{\displaystyle _{i}}}{k} \ \geq }{\textstyle \ \sqrt[k]{\prod\limits _{i=1}^{k}} a_{i}} \end{equation*}](https://www.maxbenjamintutor.com/wp-content/ql-cache/quicklatex.com-bf24bcb59a6d00d4aa46c043839905c5_l3.png)
![]()
Under this assumption, show that it is true for ![]() ,
,
![Rendered by QuickLaTeX.com \begin{align*} \frac{a_{1} +a_{2} +...+a_{2k}}{2k} & =\frac{\frac{a_{1} +a_{2} +...+a_{k}}{k} +\frac{a_{k+1} +a_{k+2} +...+a_{2k}}{k}}{2}\\ & \\ & \geq \frac{\sqrt[k]{a_{1} a_{2} ...a_{k}} \ +\ \sqrt[k]{a_{k+1} a_{k+2} ...a_{2k}}}{2}\\ & \\ & \geq \sqrt{\sqrt[k]{a_{1} a_{2} ...a_{k}} \ \sqrt[k]{a_{k+1} a_{k+2} ...a_{2k}}}\\ & \\ & =\sqrt[2k]{a_{1} a_{2} ...a_{2k}} \end{align*}](https://www.maxbenjamintutor.com/wp-content/ql-cache/quicklatex.com-c28d5ef7ef083ca96e1828bbd0d599d9_l3.png)
Hence, if true for ![]() , it follows that it is true for
, it follows that it is true for ![]() .
.
Now under the same assumption, show it is true for ![]() ,
,
For ![]() ,
,
(2) ![]()
We are also free to choose any ![]() we wish,
we wish,
Choose ![]() =
= ![]()
Substituting into ![]() ,
,
![Rendered by QuickLaTeX.com \begin{align*} \frac{a_{1} +a_{2} +...+\frac{a_{1} +a_{2} +...+a_{k-1}}{k-1}}{k} & \ \geq \ \left( a_{1} a_{2} ...a_{k-1}\frac{a_{1} +a_{2} +...+a_{k-1}}{k-1}\right)^{\cfrac{1}{k}}\\ & \\ \Longrightarrow \ \ \ \ \ \ \ \ \ \ \ \frac{a_{1} +a_{2} +...+a_{k-1}}{k-1} & \ \geq \ \left( a_{1} a_{2} ...a_{k-1}\frac{a_{1} +a_{2} +...+a_{k-1}}{k-1}\right)^{\cfrac{1}{k}}\\ & \\ \Longrightarrow \ \ \ \ \ \ \left(\frac{a_{1} +a_{2} +...+a_{k-1}}{k-1}\right)^{k} & \ \geq \ a_{1} a_{2} ...a_{k-1}\frac{a_{1} +a_{2} +...+a_{k-1}}{k-1}\\ & \\ \Longrightarrow \ \ \ \left(\frac{a_{1} +a_{2} +...+a_{k-1}}{k-1}\right)^{k-1} & \ \geq \ a_{1} a_{2} ...a_{k-1}\\ & \\ \Longrightarrow \ \ \ \ \ \ \ \ \ \ \ \frac{a_{1} +a_{2} +...+a_{k-1}}{k-1} & \ \geq \ \sqrt[k-1]{a_{1} a_{2} ...a_{k-1}}\\ & \end{align*}](https://www.maxbenjamintutor.com/wp-content/ql-cache/quicklatex.com-2bf414271649226e1c224d3d8dbf083e_l3.png)
Hence, if true for ![]() , it is also true for
, it is also true for ![]() .
.
Since we have proved all three conditions, it follows that the statement is true for all ![]() .
. ![]()
Note: If you are worried about the step where we choose a particular value of ![]() , that loss of generality doesn’t matter, since we have effectively ‘thrown away’
, that loss of generality doesn’t matter, since we have effectively ‘thrown away’ ![]() in the final statement.
in the final statement.
If you are feeling brave, try and redo this proof using standard induction.
